Bezier es el último de los tipos de curva sobre caminos en elementos canvas que nos queda por ver en el Manual de trabajo con el canvas del HTML 5.

El modelo que propone Bezier es un tipo de función matemática para definir curvas complejas en función de varios valores. Es una técnica utilizada en el dibujo técnico, que surgió inicialmente en el mundo de la aeronáutica y el diseño de coches y que se hizo bastante popular a raíz de su utilización en varios programas de diseño, como el conocido Photoshop. Las curvas Bezier se crean por medio de una fórmula matemática que permite especificar y evaluar trazados curvos que podrían tener más de un punto de inflexión.

Método para dibujar curvas Bezier

En el dibujo con el elemento Canvas se han implementado las curvas Bezier a partir del siguiente método del contexto del canvas.

bezierCurveTo(pc1x, pc1y, pc2x, pc2y, x, y)

Como vemos, se tienen que especificar coordenadas de tres puntos, de una manera similar a la que conocimos en las curvas cuadráticas.

En la siguiente imagen se puede ver un diagrama sobre los puntos que se utilizan para definir una curva Bezier.

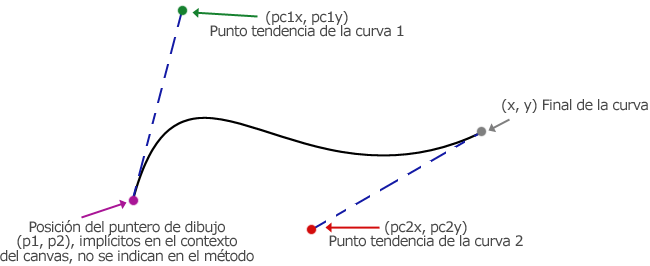
Como podemos ver, el método bezierCurveTo() tiene 6 parámetros que corresponden con las coordenadas de 3 puntos, pero en la imagen se utilizan hasta 4 puntos para definir la curva Bezier, pues el punto de incicio de la curva ya estaba en el contexto del canvas. Así que, atendiendo a la anterior imagen, estos serían los puntos necesarios para componer la curva Bezier:

1. El primer punto, marcado con color morado, es el punto inicial de la curva. Este punto no se tiene que definir, pues ya está implícito en el contexto del canvas, en el lugar donde estaba el puntero de dibujo al llamar al método bezierCurveTo().
Nota: Al dibujar cualquier segmento de un camino tenemos definido siempre de antemano el punto inicial de ese segmento del camino, pues es el lugar donde está el puntero de dibujo. Nosotros podríamos cambiar ese puntero de dibujo, para cambiar el primer punto de la curva, con una llamada al método moveTo().
2. El segundo punto, que se ha marcado de color verde, es la tendencia de la primera parte de la curva, que se indica con los parámetros pc1x, pc1y.
3. El tercero, marcado de color rojo, es la tendencia de la segunda parte de la curva, que se indica con los parámetros pc2x, pc2y.
4. Finalmente, tenemos el punto final de la curva, marcado en color gris, que se indica con los parámetros x,y.

Ejemplo de dibujo con curvas Bezier

Ahora podemos crear un ejemplo para que los lectores puedan terminar de entender las curvas Bezier. Veamos un camino que contiene alguna recta y varias curvas Bezier.

var ctx = cargaContextoCanvas('micanvas');
if(ctx){
   ctx.beginPath();
   ctx.fillStyle = "#ccccff";
   ctx.moveTo(0,40);
   ctx.bezierCurveTo(75,17,70,25,100,60);
   ctx.bezierCurveTo(130,35,140,45,145,50);
   ctx.bezierCurveTo(180,45,190,55,200,70);
   ctx.lineTo(200,150);
   ctx.lineTo(0,150);
   ctx.fill();
}

La curva anterior se puede ver representada en una página aparte.

Ahora podemos complicar un poco más ese ejemplo para crear otros caminos con curvas Bezier, con la particularidad de que vamos a rellenarlos con colores semitransparentes.

ctx.fillStyle = "#ccccff";

ctx.fillStyle = 'rgba(100,230,100,0.3)';

ctx.beginPath();
ctx.fillStyle = 'rgba(100,230,100,0.3)';
ctx.moveTo(0,90);
ctx.bezierCurveTo(90,7,110,15,140,30);
ctx.bezierCurveTo(130,55,140,65,145,70);
ctx.bezierCurveTo(180,45,190,55,200,95);
ctx.lineTo(200,150);
ctx.lineTo(0,150);
ctx.fill();

ctx.beginPath();
ctx.fillStyle = 'rgba(230,230,100,0.3)';
ctx.moveTo(50,150);
ctx.bezierCurveTo(90,7,110,15,160,10);
ctx.bezierCurveTo(130,105,140,135,200,35);
ctx.lineTo(200,150);
ctx.lineTo(0,150);
ctx.fill();

Creando esos otros caminos el ejemplo queda como se puede ver en este enlace http://www.desarrolloweb.com/articulos/ejemplos/html5/bezier-curve.html.